MIRR (Modified Internal Rate of Return) Function

The MIRR function in Weissr works similarly to Excel's MIRR function. It calculates the modified internal rate of return for a series of cash flows while factoring in both the cost of investment (finance rate) and the reinvestment rate for cash inflows. Unlike the standard IRR function, MIRR provides a more realistic measure of investment performance by addressing different borrowing and reinvestment rates.

Syntax

=MIRR(values, finance_rate, reinvest_rate)

  • values: An array or range of cells representing the series of cash flows. This includes initial investment (negative value) and subsequent cash inflows (positive values).

  • finance_rate: The interest rate you pay on the money invested (cost of financing).

  • reinvest_rate: The rate of return you earn on reinvested cash inflows.

Calculation Steps

  1. Separate Cash Flows:

    • Identify and discount negative cash flows (outflows) to the start of the period (time 0) using the finance rate.

    • Identify and compound positive cash flows (inflows) to the end of the period using the reinvestment rate.

  2. Calculate Terminal Values:

    • Compute the Present Value (PV) of outflows using the finance rate.

    • Compute the Future Value (FV) of inflows using the reinvestment rate.

  3. Find the Rate:

    • Solve for the rate (MIRR) that equates the present value of outflows and the future value of inflows over the total number of periods.

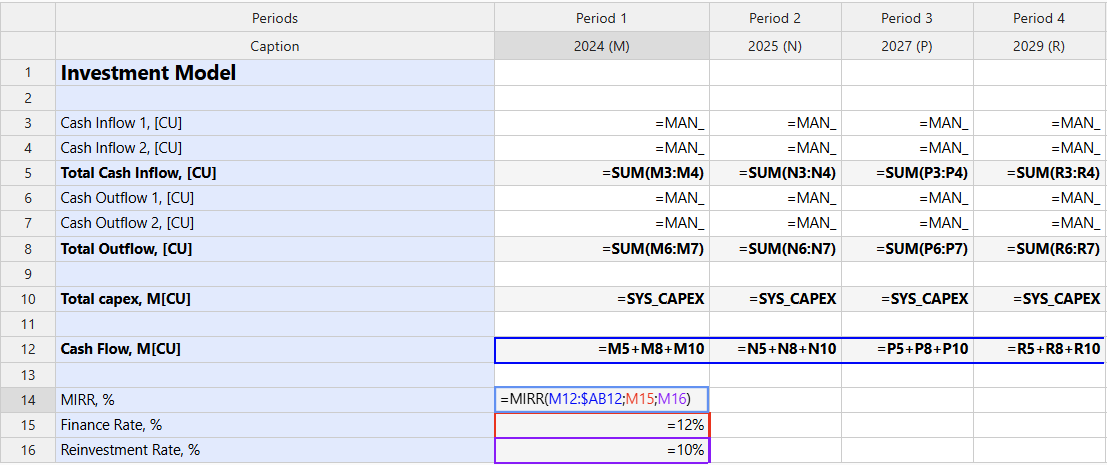
Model Configuration in Weissr

When using MIRR in a Capex Strategy Project or Capex Management:

  • For a row in Model Builder, input the formula in your preferred Period. To be able to utilize this value in Properties in Capex Management the formula must be input in Period 1

  • Note: The range of the formula depends on your project settings. For Capex Management, the model has a fixed period of 16 years in the Model Builder.

Example Formula

=MIRR(M12:OFFSET($AB12;0);M15;M16)

When this formula is entered, it automatically resolves as:

=MIRR(M13:$AB$13, M16, M17)

The OFFSET function ensures the formula dynamically references the correct end year based on the model’s analysis period.

Formula Components

  • M13:$AB$13: Represents the range of cash flows.

  • M16: The finance rate.

  • M17: The reinvestment rate.

Be cautious when defining the cash flow range. The range should align with the analysis period to avoid calculation errors.

image-20241128-153938.png
Example of the MIRR Function in the Model Builder.

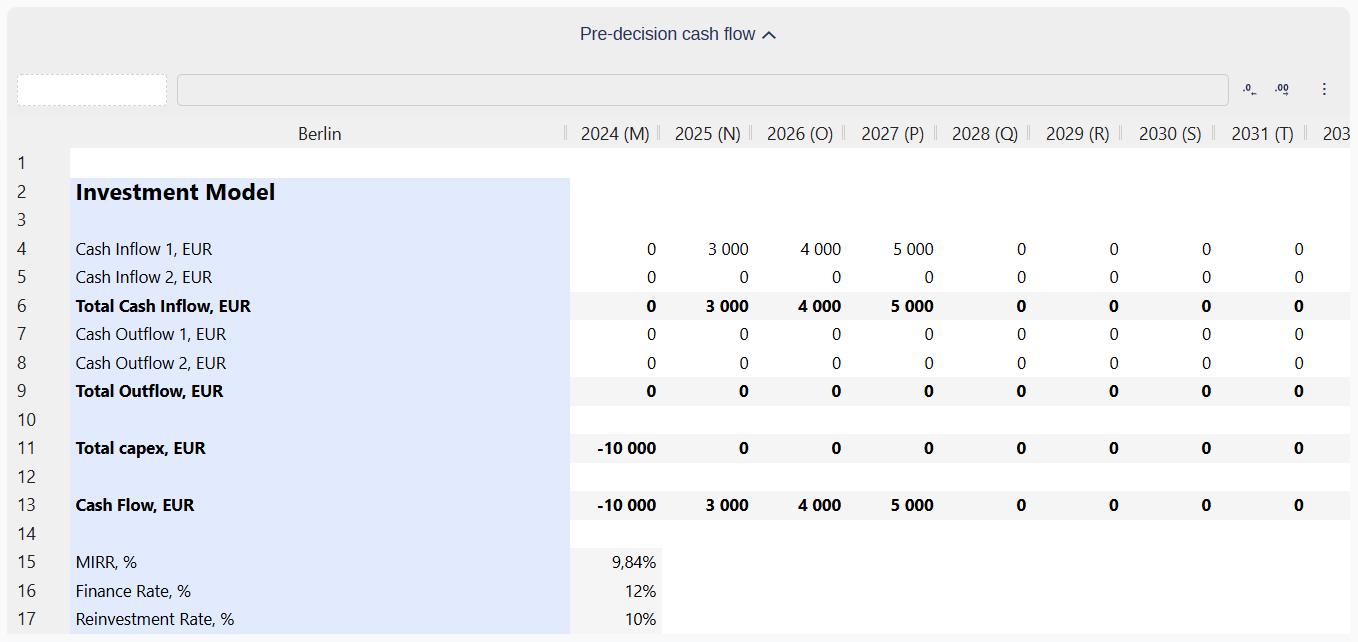
Example

Cash Flow Details

  • Cash Flows: -10,000 (initial investment), 3,000, 4,000, 5,000

  • Finance Rate: 10%

  • Reinvestment Rate: 12%

Steps

  1. Present Value of Outflows (PV):

    • The initial investment is already at time 0, so no discounting is needed: PV = -10,000.

  2. Future Value of Inflows (FV):

    • Compound the cash inflows (3,000, 4,000, and 5,000) to the final period at the reinvestment rate of 12%.

  3. Result:

    • MIRR calculates the annualized rate of return for the investment.

image-20241128-160402.png
Example of the MIRR Function in a cash flow model.

Key Notes

  • Unlike IRR, MIRR provides a single solution regardless of the sequence or magnitude of cash flows.

  • MIRR assumes reinvestment at a specified rate, which can be more realistic than IRR’s implicit assumption of reinvestment at the IRR itself.

By using MIRR, you can account for both the cost of funds and the potential profitability of reinvesting returns, giving a more comprehensive view of investment performance.

Search